Las columnas se definen como miembros que transmiten cargas axiales de compresión. Las columnas, por lo común, fallan por pandeo, que es una forma de inestabilidad. El modelo conceptual es el de un miembro perfectamente recto, y cargado en el centro sin, sin cargas laterales ni momentos flexionantes. Nosotros seguiremos el análisis original de Euler. La figura 11.1 muestra el eje estructural de un miembro movido de su original posición recta mediante un pequeño desplazamiento (esta muy ampliado). El problema matemático consiste en encontrar la carga axial “crítica” a la cual la columna permanecerá en equilibrio estático en la posición desplazada. La solución del problema determinará también la forma de la curva de la deflexión.
En la configuración desplazada, la presencia de la carga axial P produce momentos flexionantes de magnitud PH. Estos momentos ocasionan desplazamientos de flexión. Postulamos que, para una carga crítica Per, los momentos serán tales que la columna permanecerá en la posición desplazada (establece en forma neutra). En esta condición, la columna no puede soportar, estáticamente una carga adicional; se flexionará indefinidamente.
La única ecuación física necesaria es la de la ecuación, que, para desplazamientos pequeños desde una configuración recta, puede aproximarse adecuadamente por la relación:
El signo negativo es importante, quiere decir que los momentos mostrados en la figura 11.1c causan una disminución de la pendiente sobre una longitud dx, puesto que ϕ, puede ser expresada mediante dy/dx,
Pero M=Py. Sustituyendo, se obtiene:
Esta ecuación diferencial significa que y es una función de x tal que su segunda derivada es igual a –y multiplicada por el término constante P/EI.
Una manera de resolver este tipo de ecuación diferencial consiste en ponerla en la forma
En donde, p2 = P/EI. La solución general de (d) es
En dónde C1 y C2 son constantes de integración. Para evaluar estas constantes se utilizan las condiciones de frontera. Sustituyendo en la ecuación (e), se obtiene
Por tanto C2 = 0 y la ecuación (e) se convierte en
En x = L, y = 0; en la Ec. (f) bien sea C1 o p deben tener un valor tal que
En donde C1 es la amplitud de una semionda, es decir, el desplazamiento debido a flexión, ala mitad de la longitud. Una solución fácil es C1 = 0, es decir, la columna permanecerá recta. Cuándo C1 no es cero el valor de sen pL será cero solo cuándo, pL=0, π, 2π…..nπ (en dónde n es un número entero). Por tanto y = 0 en x = L cuándo
Para encontrar Per , el valor de P para el cuál esto es posible se eleva al cuadrado la Ec. (h), obteniendo
Si se sustituye en lugar de p2 su valor P/EI se obtiene
Cuando n=0, Per=0 (solución trivial). El más pequeño valor de P para el cual el pandeo es posible, ocurre cuándo n=1.
En la Ec. (i), n representa el número de semiondas. Cuándo n=2 la columna se pandea en forma de S y la carga crítica es cuatro veces mayor a la correspondiente al caso de n=1. Sin embargo, sin apoyo externo a la mitad del claro la columna no podrá desarrollar esta configuración.
Haciendo que PE represente carga de Euler, para una columna doblemente articulada, se obtiene
Esta es la Ec. Fundamental en la teoría del pandeo. Deben observarse en especial, los siguientes aspectos.
1.- La carga fundamental de Euler corresponde a una columna articulada en cada extremo, con los extremos restringidos lateralmente de modo que su movimiento relativo (acortamiento de la columna) ocurre a lo largo del eje de carga (veáse la figura 11.1)
2.- La flexión ocurre con respecto al eje principal para que el momento de inercia es un mínimo; la articulación está colocada en forma correspondiente al eje neutro.
3.- El esfuerzo normal P/A permanece en el rango elástico.
4.- La sección transversal no varía en forma o tamaño sobre la longitud de la columna.
5.- Los desplazamientos axiales no intervienen en la solución, sin embargo, la columna como un todo, se acorta como resultado de la flexión cuando ocurre el pandeo.
6.- Se omiten los desplazamientos laterales debidos a las fuerzas cortantes. Esta simplificación solo causa errores insignificantes a no ser que la columna sea relativamente “débil” (es decir, no rígida) en cortante. Tales desplazamientos pueden incluirse en la teoría mediante adecuadas modificaciones.
7.- El pandeo es un fenómeno de fuerza-desplazamiento. (Esto pasa a menudo, inadvertido porque las formulas de pandeo se expresan, generalmente en términos de esfuerzo.)
8.- La aproximación de “desplazamiento pequeño” (usando dx en lugar de ds) da como resultado que Per sea independiente del desplazamiento lateral. Para desplazamiento grande, una teoría más adecuada demuestra que eso no es cierto. La carga aumenta lentamente más allá de Per, en el desplazamiento lateral. (Euler resolvió también este problema)
El método anterior usado en la derivación de la carga de pandeo, puede calificarse como una solución de valores característicos. Otros métodos son posibles, por ejemplo, el prob. 11.1 ilustra el uso directo de la ecuación de equilibrio para un caso simple. Para situaciones más complicadas se suele emplear una solución de tipo de energía, usando la ley de la conservación de la energía.
La carga de pandeo puede convertirse en el esfuerzo de pandeo dividiéndola entre el área de la sección transversal:
Se puede sustituir I/A por la identidad
En donde p es el radio de giro medido a partir del eje neutro. Se acostumbra a dividir L entre p para obtener la relación de esbeltez, L/p. ( A veces se usa r en lugar de p.) La Ec. (a) se escribe entonces
Este es el esfuerzo de Euler para una columna elástica articulada en ambos extremos. Puesto que el esfuerzo de pandeo de Euler está regido por una relación adimensional (la relación de esbeltez), dos columnas cualesquiera que tengan el mismo E, y sean semejantes en dimensiones, tendrán el mismo esfuerzo de pandeo.
Cuándo se dibuja la Ec. (11.2) como σE contra L/p, se obtiene una sola curva para cada material diferente, como se muestra en la figura 11.2
Fuentes de Información para Unidad 5:
Gere James M. y Timoshenko Stephen P.,
Singer Ferdinan L.,
Resistencia de Materiales,
Ed. HARLA
Mecánica de Materiales,
Ed. Grupo Editorial Iberoamerica
Ed. Grupo Editorial Iberoamerica
Singer Ferdinan L.,
Resistencia de Materiales,
Ed. HARLA
Beer and Johnston,
Mecánica de Materiales,
Ed. Mc Graw Hill
Rusel Hibbeler,
Mecánica de Materiales,
Ed. Pretince Hall
Fuente: http://www.itescam.edu.mx/principal/webalumnos/sylabus/asignatura.php?clave_asig=MTF-0529&carrera=IMCT-2005-284&id_d=90
Mecánica de Materiales,
Ed. Mc Graw Hill
Rusel Hibbeler,
Mecánica de Materiales,
Ed. Pretince Hall
Fuente: http://www.itescam.edu.mx/principal/webalumnos/sylabus/asignatura.php?clave_asig=MTF-0529&carrera=IMCT-2005-284&id_d=90






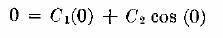






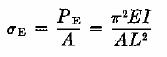





muy buena comparación de diferentes materiales en pandeo
ResponderEliminar